জ্যামিতিতে, কোণ হল দুটি রেখাংশের মধ্যকার সংযোগবিন্দু থেকে উৎপন্ন বিন্দু থেকে উৎপন্ন দুইটি দিক। কোণকে দুটি রেখাংশের মধ্যবর্তী কোণ বলেও বলা হয়।
কোণের পরিমাপ ডিগ্রিতে প্রকাশ করা হয়। একটি সমকোণ হল ৯০ ডিগ্রির কোণ। একটি বর্গক্ষেত্রের প্রতিটি কোণ সমকোণ। একটি সমবাহু ত্রিভুজের প্রতিটি কোণ ৬০ ডিগ্রির কোণ।
কোণকে বিভিন্ন শ্রেণীতে বিভক্ত করা যায়। যেমন,
- কোণের প্রকারভেদ:
- সূক্ষ্মকোণ: ৯০ ডিগ্রির চেয়ে ছোট কোণকে সূক্ষ্মকোণ বলে।
- স্থূলকোণ: ৯০ ডিগ্রির চেয়ে বড় কোণকে স্থূলকোণ বলে।
- সমতলকোণ: ৯০ ডিগ্রি কোণকে সমতলকোণ বলে।
- সমকোণ: ৯০ ডিগ্রি কোণকে সমকোণ বলে।
- অসমকোণ: ৯০ ডিগ্রি কোণ ছাড়া অন্য কোণকে অসমকোণ বলে।
- কোণের অবস্থানভেদে:
- অভ্যন্তরীণ কোণ: ত্রিভুজের তিনটি শীর্ষবিন্দুর মধ্যবর্তী কোণগুলোকে অভ্যন্তরীণ কোণ বলে।
- বাহ্যিক কোণ: ত্রিভুজের একটি শীর্ষবিন্দু এবং তার বিপরীত বাহুর শেষবিন্দু থেকে উৎপন্ন কোণকে বাহ্যিক কোণ বলে।
কোণ জ্যামিতির একটি গুরুত্বপূর্ণ ধারণা। কোণের সাহায্যে বিভিন্ন জ্যামিতিক আকৃতি এবং তাদের বৈশিষ্ট্যগুলি নির্ণয় করা যায়।

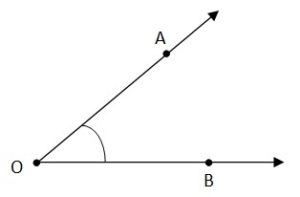 কোণ (Angle)
কোণ (Angle) 